Freym PC Blog

La hipótesis de Riemann

La hipótesis de Riemann sigue siendo uno de los problemas más fascinantes y esquivos de las matemáticas modernas. Hasta el 1 de marzo de 2025, no ha sido demostrada ni refutada, por lo que permanece como una de las conjeturas abiertas más importantes, incluida en los Problemas del Milenio del Instituto Clay, con un premio de un millón de dólares para quien la resuelva.

Fue propuesta por Bernhard Riemann en 1859, está relacionada con la distribución de los números primos y se centra en los ceros no triviales de la función zeta de Riemann. Dice que todos estos ceros tienen una parte real igual a 1/2, es decir, están en la línea crítica del plano complejo. Esto tiene implicaciones profundas en la teoría de números, especialmente en cómo se comportan los primos a medida que los números crecen.

Las funciones L y su relación

Las funciones L son generalizaciones de la función zeta de Riemann, asociadas a representaciones de grupos (como en el programa Langlands) o a objetos matemáticos como curvas elípticas. Una función L típica tiene una forma similar a 𝜁(𝑠)ζ(s), con un producto de Euler sobre primos y una conjetura análoga a la hipótesis de Riemann: sus ceros no triviales también estarían en una línea crítica (generalmente 𝜎=1/2σ=1/2).

La conjetura análoga: Hipótesis de Riemann generalizada

La hipótesis de Riemann generalizada (HRG) para funciones L afirma que todos los ceros no triviales de 𝐿 ( 𝑠 , 𝜒 ) L(s,χ) tienen parte real 𝜎 = 1 / 2 σ=1/2, al igual que en la hipótesis de Riemann para 𝜁 ( 𝑠 ) ζ(s). Los ceros no triviales son aquellos que no provienen de polos o ceros triviales definidos por la ecuación funcional de la función L. Para 𝐿 ( 𝑠 , 𝜒 ) L(s,χ), la ecuación funcional conecta 𝐿 ( 𝑠 , 𝜒 ) L(s,χ) con 𝐿 ( 1 − 𝑠 , 𝜒 ‾ ) L(1−s, χ ​ ), y los ceros triviales suelen estar en puntos específicos (como enteros negativos), dependiendo de si 𝜒 χ es par o impar.

Si la HRG es cierta, implica que los ceros de 𝐿 ( 𝑠 , 𝜒 ) L(s,χ) están alineados en la línea crítica 𝜎 = 1 / 2 σ=1/2, lo que controla la distribución de términos como 𝜒 ( 𝑝 ) 𝑝 − 𝑠 χ(p)p −s en el producto de Euler. Esto tiene consecuencias en teoría de números, como la distribución de primos en progresiones aritméticas (por ejemplo, primos de la forma 𝑎 + 𝑞 𝑛 a+qn), ya que el comportamiento oscilatorio de 𝐿 ( 𝑠 , 𝜒 ) L(s,χ) está gobernado por estos ceros.

Diferencias en la analogía

Aunque la hipótesis de Riemann y su versión generalizada para funciones L comparten la idea de ceros en la línea crítica, hay diferencias clave:

1. Estructura del carácter ( 𝜒 χ) vs. ausencia de carácter:

  • En 𝜁 ( 𝑠 ) ζ(s), el producto de Euler es "puro": cada término 1 − 𝑝 − 𝑠 1−p −s es uniforme para todos los primos. En 𝐿 ( 𝑠 , 𝜒 ) L(s,χ), el carácter 𝜒 ( 𝑝 ) χ(p) introduce una dependencia del primo 𝑝 p módulo 𝑞 q. Por ejemplo, si 𝜒 χ es un carácter no trivial, 𝜒 ( 𝑝 ) = 0 χ(p)=0 para 𝑝 p divisor de 𝑞 q, y para otros primos puede ser una raíz de la unidad (como 𝑒 2 𝜋 𝑖 𝑘 / 𝑞 e 2πik/q ).
  • Diferencia: Esto hace que 𝐿 ( 𝑠 , 𝜒 ) L(s,χ) sea más "especializada" que 𝜁 ( 𝑠 ) ζ(s), enfocándose en subconjuntos de primos o en sus propiedades cíclicas, mientras que 𝜁 ( 𝑠 ) ζ(s) abarca todos los primos sin filtrar.

    • 2. Ceros triviales y ecuación funcional:

  • Para 𝜁 ( 𝑠 ) ζ(s), los ceros triviales están en 𝑠 = − 2 , − 4 , − 6 , … s=−2,−4,−6,…, derivados de su ecuación funcional 𝜁 ( 𝑠 ) = 2 𝑠 𝜋 𝑠 − 1 sin ⁡ ( 𝜋 𝑠 / 2 ) Γ ( 1 − 𝑠 ) 𝜁 ( 1 − 𝑠 ) ζ(s)=2 s π s−1 sin(πs/2)Γ(1−s)ζ(1−s).
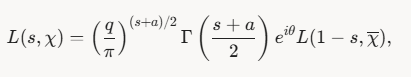
  • Para 𝐿 ( 𝑠 , 𝜒 ) L(s,χ), la ecuación funcional depende de 𝜒 χ. Por ejemplo, si 𝜒 χ es un carácter primitivo módulo 𝑞 q, la ecuación es:
    • Ecuación

    donde 𝑎 = 0 a=0 o 1 1 según la paridad de 𝜒 χ, y 𝜃 θ es una constante. Los ceros triviales cambian de posición y naturaleza según 𝜒 χ.

  • Diferencia: La posición y cantidad de ceros triviales varía, lo que afecta cómo se identifican los ceros no triviales en 𝐿 ( 𝑠 , 𝜒 ) L(s,χ) frente a 𝜁 ( 𝑠 ) ζ(s).

    • 3. Simetrías y complejidad:

  • ζ(s) tiene una simetría simple: 𝜁 ( 𝑠 ) = 𝜁 ( 𝑠 ‾ ) ‾ ζ(s)= ζ( s ) ​ , y su comportamiento es universal para todos los primos.
  • En 𝐿 ( 𝑠 , 𝜒 ) L(s,χ), el carácter 𝜒 χ introduce simetrías adicionales (por ejemplo, 𝜒 ( 𝑛 ) = 1 χ(n)=1 o − 1 −1 en ciertos casos), y si 𝜒 χ es real, 𝐿 ( 𝑠 , 𝜒 ) L(s,χ) puede tener ceros en la línea real (como 𝑠 = 1 / 2 s=1/2) que 𝜁 ( 𝑠 ) ζ(s) no tiene.
  • Diferencia: Algunos 𝐿 ( 𝑠 , 𝜒 ) L(s,χ) con 𝜒 χ real tienen ceros "extra" (llamados ceros de Siegel) en 0 < 𝜎 < 1 0<σ<1, fuera de la línea crítica pero dentro de la tira crítica, algo que no ocurre en 𝜁 ( 𝑠 ) ζ(s). Esto complica la analogía, ya que la HRG no siempre cubre estos casos.

    • 4. Aplicaciones numéricas:

  • Los ceros de 𝜁 ( 𝑠 ) ζ(s) se calculan en la línea 𝜎 = 1 / 2 σ=1/2 y se verifica su densidad (aproximadamente 𝑇 log ⁡ 𝑇 2 𝜋 2π TlogT ​ ceros hasta altura 𝑇 T). Todos los ceros encontrados son complejos.
  • Para 𝐿 ( 𝑠 , 𝜒 ) L(s,χ), los ceros también se buscan en 𝜎 = 1 / 2 σ=1/2, pero si 𝜒 χ es real, pueden aparecer ceros reales (como 𝑠 = 0.5 + 0 𝑖 s=0.5+0i) que violan la expectativa de oscilación pura. Por ejemplo, para el carácter 𝜒 ( 𝑛 ) = ( − 3 / 𝑛 ) χ(n)=(−3/n) (símbolo de Legendre), se han calculado ceros reales en ciertos casos.
  • Diferencia: La posibilidad de ceros reales en 𝐿 ( 𝑠 , 𝜒 ) L(s,χ) introduce una excepción potencial a la HRG que no existe en 𝜁 ( 𝑠 ) ζ(s), haciendo la analogía imperfecta.

    • Freym PC Podcast

    Back | Main | Next | End